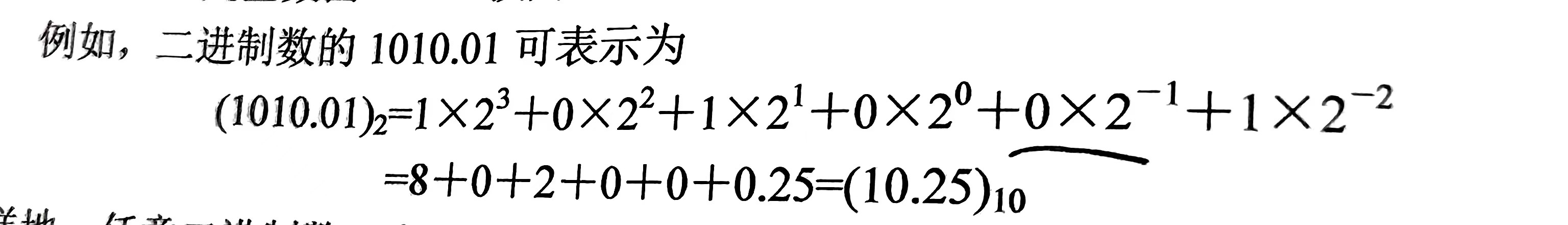第一章

1.1 数制转换:

==全是带小数部分的题==

1.1.1 十进制数写成幂的形式:

1.1.2 二进制带小数部分转换十进制

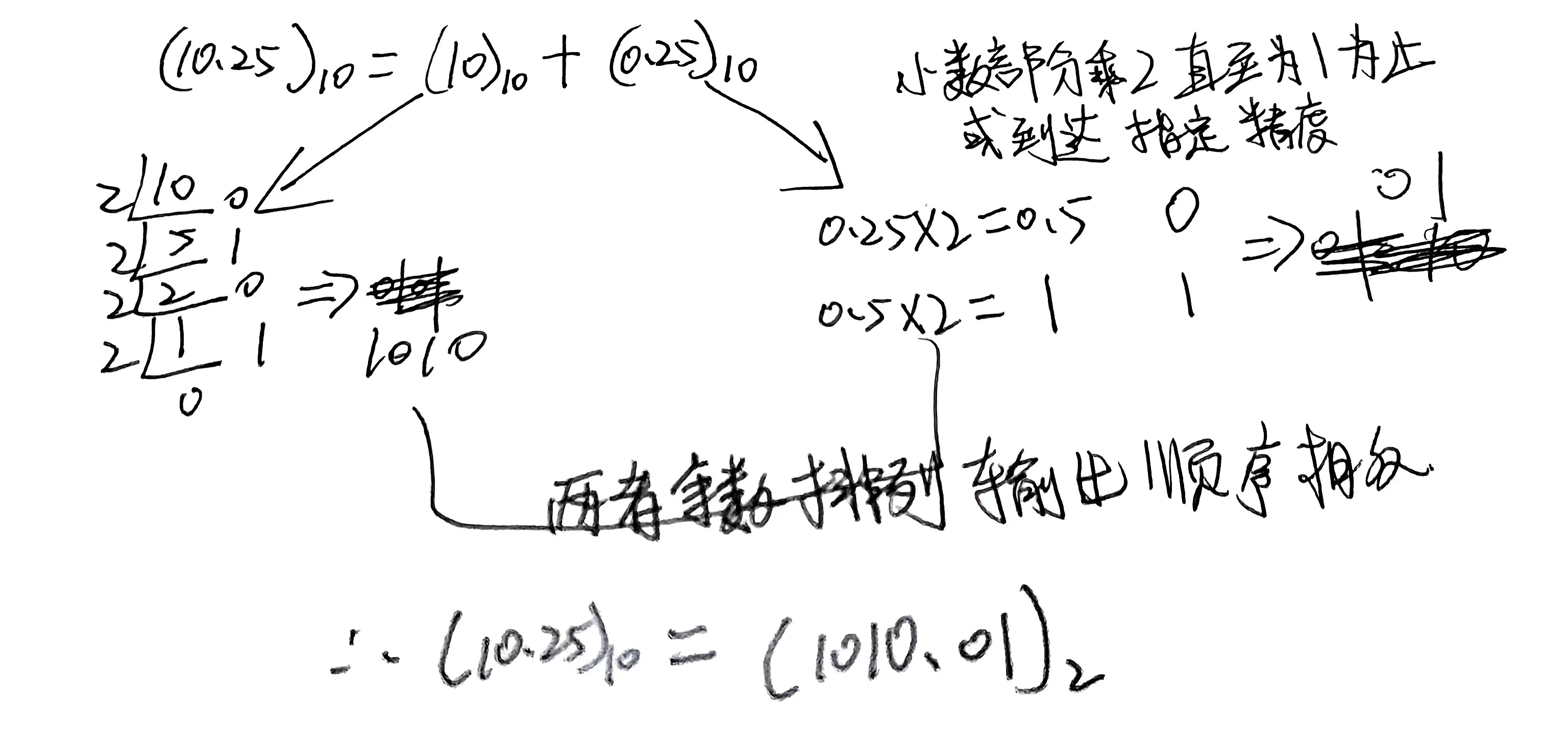
1.1.3 十进制带小数部分转换二进制

1.1.4 二进制带小数转换八进制/八进制带小数转二进制

1.1.5 二进制带小数部分转十六进制/十六进制带小数部分转二进制

1.2 编码

1.2.1 8421码

==针对十进制数，先全部化成十进制数，再把十进制数化成二进制==

8421码的计算以及余三码的计算

第二章

==①反函数、对偶、卡诺图、求最小项==

2.1 对偶式

2.2 求最小项

2.3 卡诺图

2.4 异或\同或

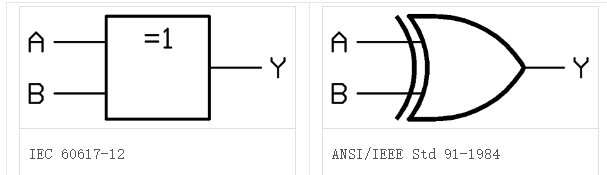
注意简单能够认识这两个的电路表示图

2.4.1 同或

==定义:指两个输入变量取值相同时输出1，取值不相同输出0，其运算符号为⊙==

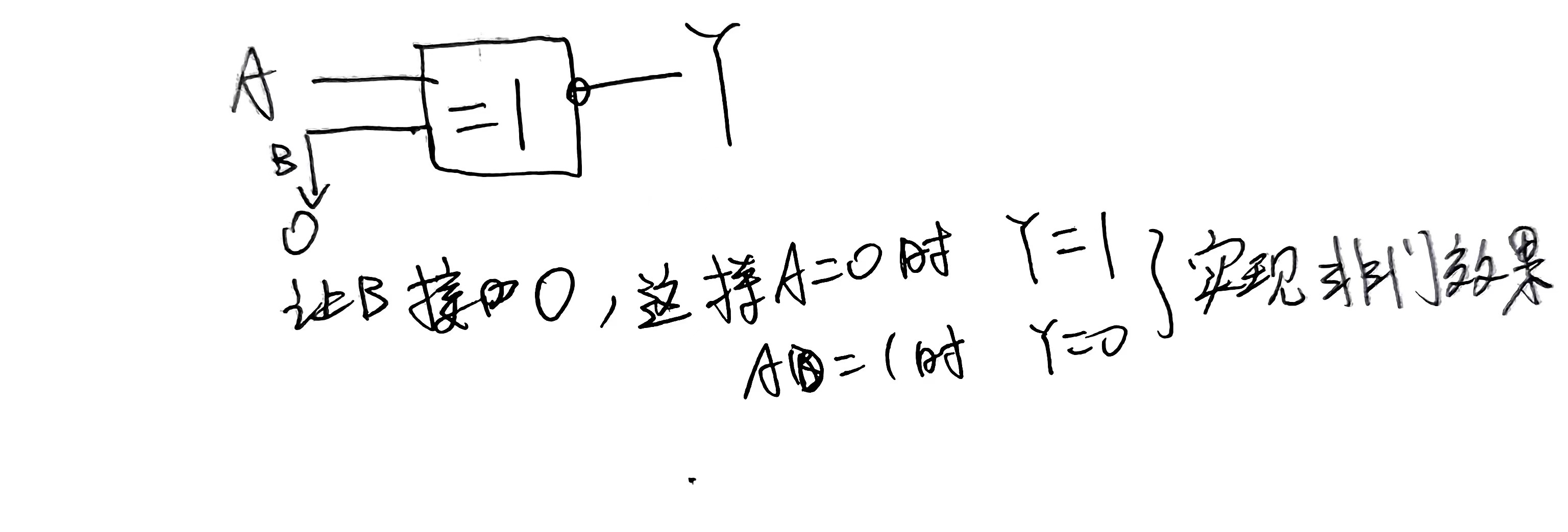
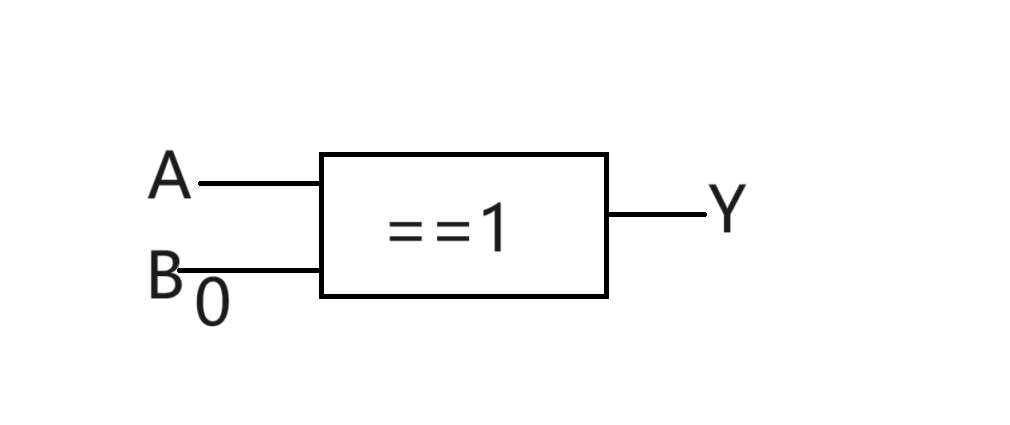
2.4.2 异或

==定义:指两个输入变量取值相同时输出为0，取值不相同时输出为1，其运算符号为⊕==

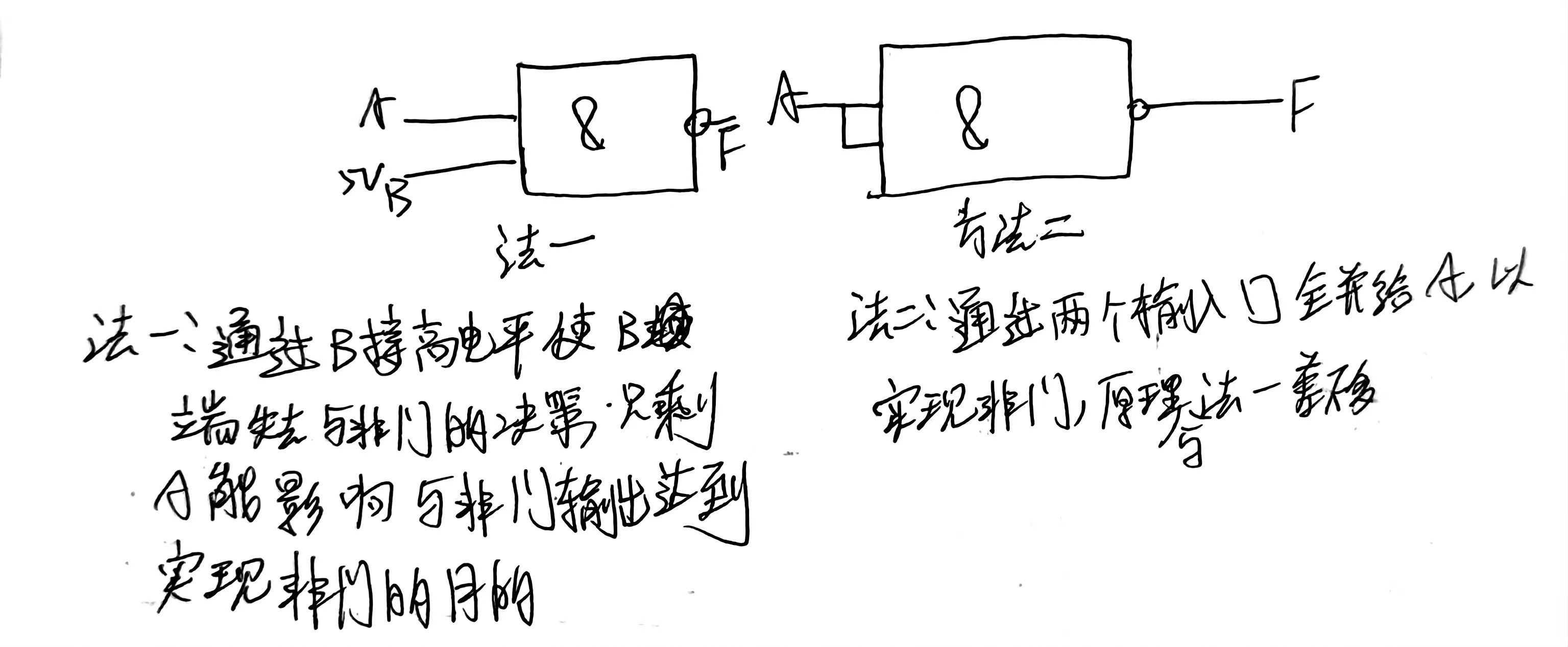
2.5 转换非门

2.5.1 与非门实现非门

2.5.2 或非门实现非门

2.5.3 同或门实现非门

2.5.4 异或门实现非门

第四章

编码器:对M个信号编码时,应如何确定位数N？

　　编码原则：N位二进制代码可以表示$2^N$个信号，则对M个信号编码时，应由$2^N≥M$来确定位数N。

　　例：对101键盘编码时，采用了7位二进制代码ASCⅡ码。$2^7=128＞101$

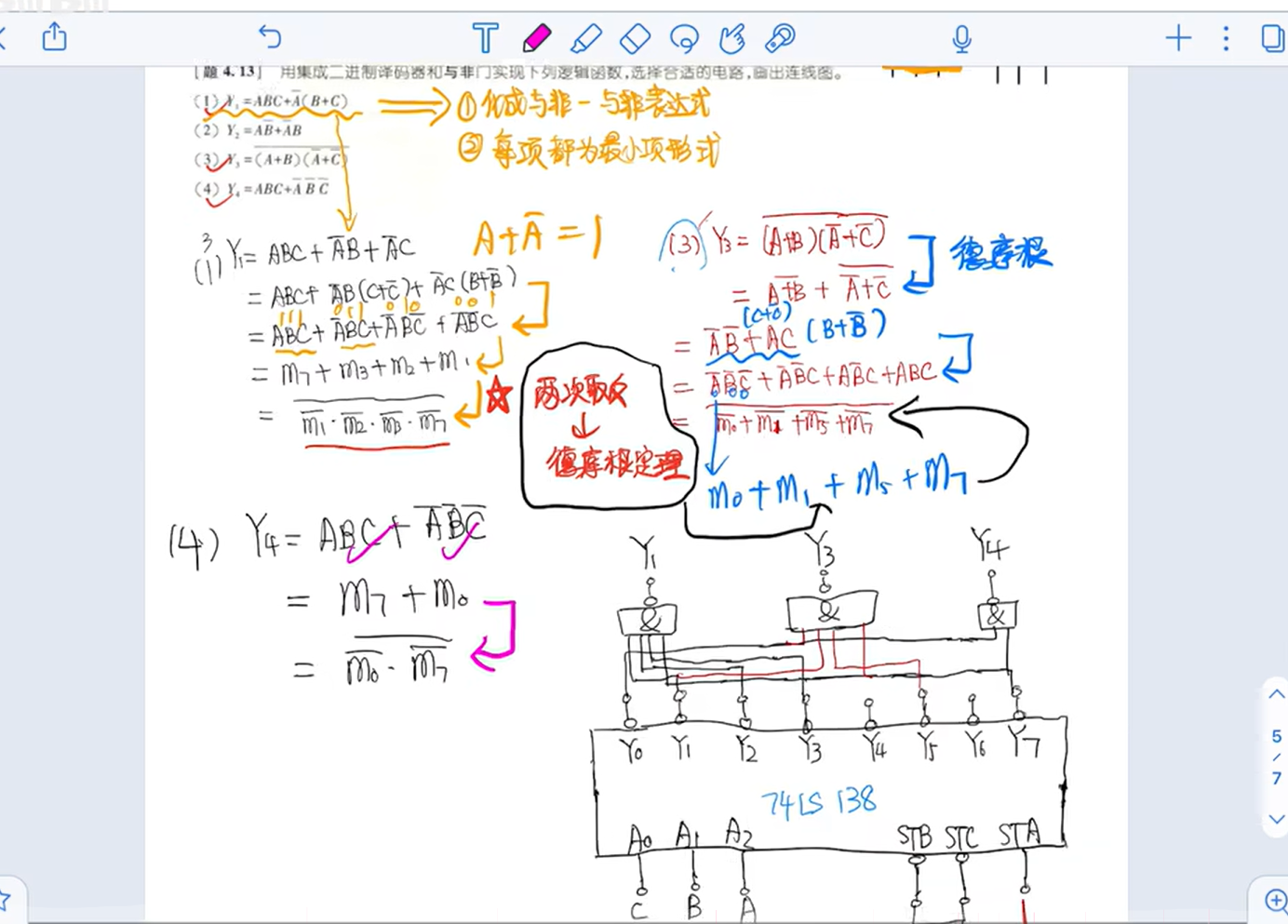
==译码器==

当 i 不等于 j 时，同一逻辑函数的两个最小项 ( m_i ) 和 ( m_j ) 的逻辑与 $( m_i \cdot m_j )$ 等于 0。这是因为每个最小项代表了一组特定的输入变量的状态，当这些状态不同时，不可能同时满足两个最小项的条件，因此它们的逻辑与结果是假（0）。

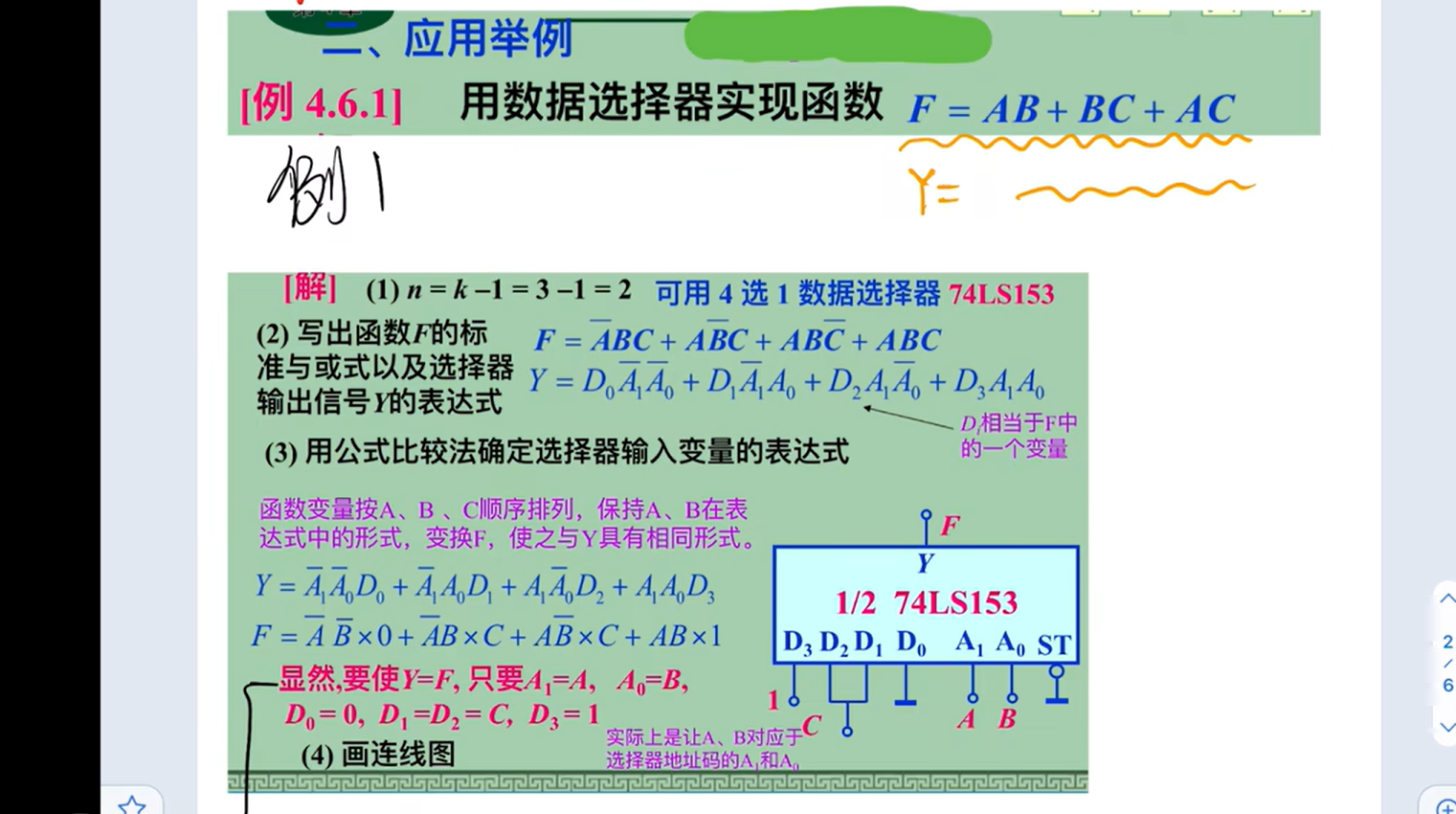
==数据选择器==

第五章

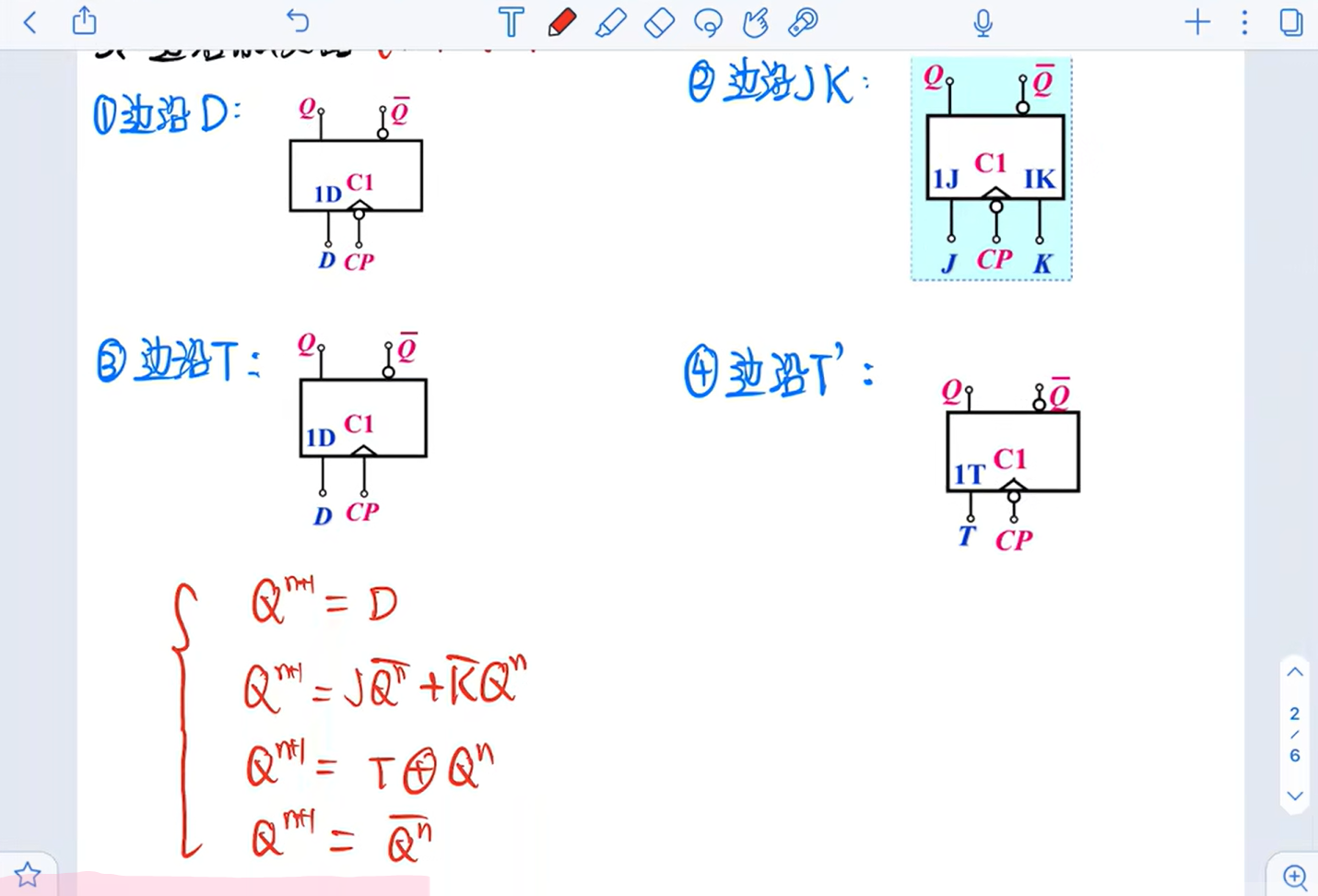
同步触发器

JK触发器

边沿D触发器

第六章

==同步时序逻辑电路的分析举例:==

①:写相关方程

②时钟方程

==74LS161芯片进行计数:==

清零法

置数法

同步预置法

==单向移位寄存器==

第八章

数/模转换

第九章

寄存器：

RAM:具有随机存取的功能

ROM:只具备只读的功能

74LS153芯片:判奇判偶

---

• 分类： 未分类
• 标签： 无标签